√完了しました! (a+b+c)^3 expansion 192844-What is a^3+b^3+c^3
$$(a b c)^3 = (a^3 b^3 c^3) 3(a b c)(ab ac bc) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3(a b c)(ab ac bc) abc$$ It doesn't look like I made careless mistakes, so I'm wondering if the statement asked is correct at allThe third power of the trinomial a b c is given by ( a b c ) 3 = a 3 b 3 c 3 3 a 2 b 3 a 2 c 3 b 2 a 3 b 2 c 3 c 2 a 3 c 2 b 6 a b c {\displaystyle (abc)^{3}=a^{3}b^{3}c^{3}3a^{2}b3a^{2}c3b^{2}a3b^{2}c3c^{2}a3c^{2}b6abc}A^3 b^3 c^3 plus 3 of each term having one variable and another one squared like ab^2, b^2c, all 6 combinations of those, then plus 6abc and that's it

Misc 1 Find A B N In Expansion Of A B N If First Three
What is a^3+b^3+c^3
What is a^3+b^3+c^3-BACK TO EDMODO Menu Find a quiz All quizzes All quizzes My quizzes Reports Create a new quiz 0 Join a game Log in Sign up View profile Have an account?Expand (a – b – c d) 10 using multinomial theorem and by using coefficient property we can obtain the required result Using multinomial theorem, we have We want to get coefficient of a 3 b 2 c 4 d this implies that r 1 = 3, r 2 = 2, r 3 = 4, r 4 = 1, ∴ The coefficient of a 3 b 2 c 4 d is (10)!/(3!2!4) (1) 2 (1)4 =



Solved Show That Det 1 1 1 1 A B C D A 2 B 2 C 2 D 2 A 3 Chegg Com
(abc) 3 a 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 terms We can choose two a's from 3 factors in C(3,2) ways=3Perimeter = abc Area of equilateral triangle = 3 4 a2 Sphere Surface Area = 4πr2;3 a) truth table b) sop y0 = (a'b'c'd)(a'b'cd')(a'bc'd')(a'bcd)(ab'c'd')(ab'cd)(abc'd)(a bcd') y1= (a'b'cd)(a'bc'd
Proof Formula \((abc)^3 = \\a^3 b^3 c^3 6abc \\ 3ab (ab) 3ac (ac) 3bc (bc) \) Summary (abc)^3 If you have any issues in the (abc)^3 formulas, please let me know through social media and mail A Plus B Plus C Whole cube is most important algebra maths formulas for class 6 to 12Now, if you name the equal pairs of angles in each isosceles triangle, A, A, B, B, C, C, you find that the original triangle has one angle A B, one angle B C, and one angle A C The three angles total 2A 2B 2C This, you know, adds up to 180 degrees In any isosceles triangle, the angle at the apex is 180 degrees minus twice the baseFind the maxterm expansion of F = ( A B' ) ( A' C ) b) Use XX' = 0 to introduce missing variables in each term Therefore F = = = Minterm and maxterm expansions are unique, therefore can prove equation F = G is valid by finding minterm or maxterm expansions of both sides, and demonstrating the equality
231 242 253 Answer Number of terms in the given expansion is nothing but the nonnegative integral solutions of the equation a b c = Total number of nonnegative integral solutions (31) C (31) = 22 C 2 = 231 The correct option is BA(BC) = (AB)C Proof If A, B and C are three variables, then the grouping of 3 variables with 2 variables in each set will be of 3 types, such as (A B), (B C) and(C A) According to associative law (A B C) = (A B) C = A (B C) = B (C A) We know that, A AB = A (according to Absorption law)Enter (A,B,C,D) in order below if A, B, C, and D are the coefficients of the partial fractions expansion of \(\displaystyle12\cdot\frac{x^34}{(x^21)(x^23x2



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



Q 14 C 31 If C 0 C
A 3 × 3 determinant `(a_1, b_1,c_1),(a_2,b_2,c_2),(a_3,b_3,c_3)` can be evaluated in various ways We will use the method called "expansion by minors" But first, we need a definition Cofactors The 2 × 2 determinant `(b_2,c_2),(b_3,c_3)` is called the cofactor of a 1 for the 3 × 3 determinant `(a_1, b_1,c_1),(a_2,b_2,c_2),(a_3,b_3,c_3)`Westward Expansion (Manifest Destiny) 25k plays Qs Westward Expansion 17k plays 10 Qs Mexico Geography k plays Quiz not found!Now we will learn to expand the square of a trinomial (a b c) Let (b c) = x Then (a b c) 2 = (a x) 2 = a 2 2ax x 2 = a 2 2a (b c) (b c) 2 = a 2 2ab 2ac (b 2 c 2 2bc) = a 2 b 2 c 2 2ab 2bc 2ca Therefore, (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca (a


2



The Number Of Distinct Terms In A B C D E
Enter (A,B,C,D) in order below if A, B, C, and D are the coefficients of the partial fractions expansion of \(\displaystyle12\cdot\frac{x^34}{(x^21)(x^23x2The calculator will find the binomial expansion of the given expression, with steps shown Show Instructions In general, you can skip the multiplication sign, so `5x` is equivalent to `5*x` In general, you can skip parentheses, but be very careful e^3x is `e^3x`, and e^(3x) is `e^(3x)`StarTechcom T1PCIEX16 Thunderbolt 3 PCIe Expansion Chassis Thunderbolt 3 to 16 x PCIe Aluminum PCIe SSD External PCIe Enclosure PCIe Slot Type Thunderbolt 3 to PCIe x16 and DisplayPort;


What Is The Formula For Math A B C 3 Math Quora
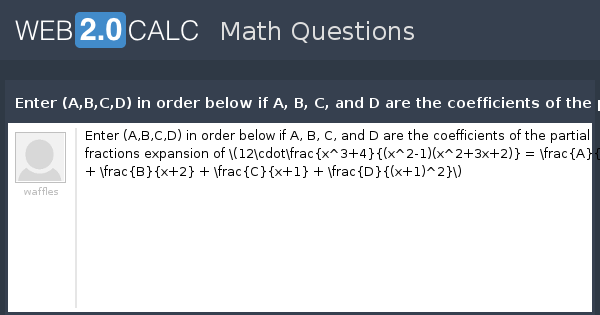


View Question Enter A B C D In Order Below If A B C And D Are The Coefficients Of The Partial Fractions Expansion Of
Related Topics Mathematics Mathematical rules and laws numbers, areas, volumes, exponents, trigonometric functions and more ;(a 3 3a 2 b 3ab 2 b 3)(ab) = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 The calculations get longer and longer as we go, but there is some kind of pattern developing That pattern is summed up by the Binomial TheoremThe expansion of (ab)^3 is(ab)^3 (a b)^3 ( a b ) ^ 3 ( a b ) ^ 3 and this will go on for ever Just write the expression on your page and see the miracle Source(s) my self 0 0 Paul Lv 7 7 years ago a^3 3a^2b 3ab^2 b^3



X A X B X C Expand And Simplify Youtube



Binomial Theorem For Any Index
• If the minterm expansion for f (A,B,C) = m 3 m 4 m 5 m 6 m 7, what is the maxterm expansion for f(A,B,C)?In Algebra In Algebra putting two things next to each other usually means to multiply So 3 (ab) means to multiply 3 by (ab) Here is an example of expanding, using variables a, b and c instead of numbers And here is another example involving some numbers Notice the "·" between the 3 and 6 to mean multiply, so 3·6 = 18We can do so in two ways The first method involves writing the coefficients in a triangular array, as follows



Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download


2
We can do so in two ways The first method involves writing the coefficients in a triangular array, as followsThe Formula is given below (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) Explanation Let us just start with (abc)² = a² b² c²2ab2bc2ca =a² b² c²2 (abbcca) now (abc)² (abc)= (a b c)³= a² b² c²2 (abbcca) (abc) =a ² abc b² abcc² abc 2 (abbcca) abcOur experiment is a splitsplit plot experiment design (including three independent variables as fixed effects, eg ABC with 3 replicates (1,2,3) and two factors, eg D E as random effects)



Solved 3 Given A B D F A B C D A B C A B D Chegg Com


Http 1 160 97 198 8080 Xmlui Bitstream Handle 758 Chapter10 Pdf Sequence 10
Volume = a 3 Cone Curved Surface Area = πrl ;Related Documents Binomial Theorem Binomial theorem for positive integers;HDPE, in general, has good impact resistance When crosslinked by any of the methods, A, B or C the HDPE overcomes some of its natural material properties, making the finished product more resilient for potable and radiant applications Always check the markings on the pipe, called the printline, for corresponding fastening methods and ratings



B 1 Cbse Notes



Total Number Of Possible Arrangements
Algebra Homework Help Expansion of (abc) 2 Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac Practice Exercise for Algebra Module on Expansion of (a b c)(a 3 3a 2 b 3ab 2 b 3)(ab) = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 The calculations get longer and longer as we go, but there is some kind of pattern developing That pattern is summed up by the Binomial TheoremVolume = 1 3 πr2 h Total surface area = πr l πr2 Cuboid Total surface area = 2 (ab bh lh);



The Binomial Theorem Lecture 29 Section 6 7 Mon Apr 3 Ppt Download



Prediction Of Expansion And Compressive Strength Loss Vs Time At 300 Download Scientific Diagram
Finally, we have (a b c)2 = a2 b2 c2 2ab 2bc 2ca In the same way, we can get idea to remember the the expansions of (a b c)3, (a b c)3 , (a b c)3 Apart from the stuff given above, if you would like to have problems on algebraic identities, please click the link given belowIf the coefficient of a 8 b 4 c 9 d 9 a^8b^4c^9d^9 a 8 b 4 c 9 d 9 in the expansion of (a b c a b d a c d b c d) 10 (abcabdacdbcd)^{10} (a b c a b d a c d b c d) 1 0 is N N N, then what is the sum of the digits of N N N equal to?The patterns we just noted indicate that there are 7 terms in the expansion a 6 c 1 a 5 b c 2 a 4 b 2 c 3 a 3 b 3 c 4 a 2 b 4 c 5 ab 5 b 6 How can we determine the value of each coefficient, c i?



Binomial Expansions 1 X N A B N N C 0 A N N C 1 A N 1 B N C 2 A



Solved Project 1 Part A You Are Tasked To Calculate A Spe Chegg Com
What I want to do with this video is cover something called the triple product expansion or Lagrange's formula, sometimes And it's really just a simplification of the cross product of three vectors, so if I take the cross product of a, and then b cross cSubmit your answer What is the coefficient of x 7 x^7 x 7 in the expansion of (1 x 2 x 3) 10A 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abc



Solved 1 Expand And Write The Following In Sop Form With Chegg Com


What Is The Formula For Math A B C 3 Math Quora
Internal Ports 1 x PCI Express x16 FemaleAlgebra Homework Help Expansion of (abc) 2 Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac Practice Exercise for Algebra Module on Expansion of (a b c)Complex Numbers Complex numbers are used in alternating current theory and in mechanical vector analysis;


Http 1 160 97 198 8080 Xmlui Bitstream Handle 758 Chapter10 Pdf Sequence 10


What Is The Expansion Of A B C 3 Quora
The binomial expansion of a difference is as easy, just alternate the signs (x y) 3 = x 3 3x 2 y 3xy 2 y 3In general the expansion of the binomial (x y) n is given by the Binomial TheoremTheorem 671 The Binomial Theorem top Can you see just how this formula alternates the signs for the expansion of a difference?Our experiment is a splitsplit plot experiment design (including three independent variables as fixed effects, eg ABC with 3 replicates (1,2,3) and two factors, eg D E as random effects)Except as otherwise provided under this subsection, the amendments made by this section amending this section and repealing section 1863 of this title shall apply with respect to investigations initiated under section 232(b) of the Trade Expansion Act of 1962 19 USC 1862(b) on or after the date of enactment of this Act Aug 23, 19


Www Tamdistrict Org Cms Lib Ca Centricity Domain 348 Adv alg ch 10 sec 5 day two completed notes Pdf



Click Here To
The third power of the trinomial a b c is given by ( a b c ) 3 = a 3 b 3 c 3 3 a 2 b 3 a 2 c 3 b 2 a 3 b 2 c 3 c 2 a 3 c 2 b 6 a b c {\displaystyle (abc)^{3}=a^{3}b^{3}c^{3}3a^{2}b3a^{2}c3b^{2}a3b^{2}c3c^{2}a3c^{2}b6abc}3 a) truth table b) sop y0 = (a'b'c'd)(a'b'cd')(a'bc'd')(a'bcd)(ab'c'd')(ab'cd)(abc'd)(a bcd') y1= (a'b'cd)(a'bc'dVolume = 4 3 πr3 Cube Surface Area = 6a2;



Solved Expand The Three Binomial Series X A X B Chegg Com



Q 16 The Total Number Of Irrational Terms In The Binomial Expansion Of Left 7 1 5 3 1 10 Right 60 Options 1 55 2 49 3 48 4 5
B) (a − b) 3 = a 3 − 3a 2 b 3ab 2 − b 3 c) ( x y ) 4 = x 4 4 x 3 y 6 x 2 y 2 4 xy 3 y 4 d) ( x − y ) 4 = x 4 − 4 x 3 y 6 x 2 y 2 − 4 xy 3 y 4Choose those not present in the minterms –So the Maxterm expansion for f(A,B,C) = M 0 M 1 M 2 Chap 4 CH10 Complement of minterm • Complement of a minterm is theDefinition binomial A binomial is an algebraic expression containing 2 terms For example, (x y) is a binomial We sometimes need to expand binomials as follows (a b) 0 = 1(a b) 1 = a b(a b) 2 = a 2 2ab b 2(a b) 3 = a 3 3a 2 b 3ab 2 b 3(a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4(a b) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5Clearly, doing this by



Solved 3 Given F A B C D A B C A B D G A B Chegg Com



Pascal S Triangle And The Binomial Theorem X Y 0 1 X Y 1 1x 1y X Y 2 1x 2 2xy 1y 2 X Y 3 1x 3 3x 2 Y 3xy 2 1 Y 3 X Ppt Download
Favourite answer You didn't specify if a,b,c are all distinct Firste note that a^3 b^3 c^3 3abc = (a b c) (a^2 b^2 c^2 ab ac bc) By assumption a^3b^3c^3=3abc so the leftThe patterns we just noted indicate that there are 7 terms in the expansion a 6 c 1 a 5 b c 2 a 4 b 2 c 3 a 3 b 3 c 4 a 2 b 4 c 5 ab 5 b 6 How can we determine the value of each coefficient, c i?External Ports 2 x Thunderbolt 3 USBC (24pin) Female 1 x DisplayPort ( pin) Female;



Multinomial Expansion



Which Formed First A Hydrogen Nuclei B Hydrogen Atoms C Heliumanswer Keya Course Hero
231 242 253 Answer Number of terms in the given expansion is nothing but the nonnegative integral solutions of the equation a b c = Total number of nonnegative integral solutions (31) C (31) = 22 C 2 = 231 The correct option is BIn mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials The expansion is given by The expansion is given by ( a b c ) n = ∑ i j k = n i , j , k ( n i , j , k ) a i b j c k , {\displaystyle (abc)^{n}=\sum _{\stackrel {i,j,k}{ijk=n}}{n \choose i,j,k}\,a^{i}\,b^{\;\!j}\;\!c^{k},}Discrete Data Sets Mean, Median and Mode Values Calculate arithmetic mean



Binomial Theorem Wikipedia



Solved 22 For The Binomial Expansion Of X Y The Va Chegg Com
Eg, F(A,B,C) = ΠM(0,2,4) = Σm(1,3,5,6,7) Minterm expansion of F to minterm expansion of F' use minterms whose indices do not appear eg, F(A,B,C) = Σm(1,3,5,6,7) F'(A,B,C) = Σm(0,2,4) Maxterm expansion of F to maxterm expansion of F' use maxterms whose indices do not appearLog in now Create a new quizHDPE, in general, has good impact resistance When crosslinked by any of the methods, A, B or C the HDPE overcomes some of its natural material properties, making the finished product more resilient for potable and radiant applications Always check the markings on the pipe, called the printline, for corresponding fastening methods and ratings



Solve This Binomial Theorem Problem If 3rd 4th 5th Amp 6th Term Are In The Expansion Of X Y N Be Brainly In


Plos One A Degree Based Block Model And A Local Expansion Optimization Algorithm For Anti Community Detection In Networks
The scalar triple product is unchanged under a circular shift of its three operands (a, b, c) a ⋅ ( b × c ) = b ⋅ ( c × a ) = c ⋅ ( a × b ) {\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )=\mathbf {b} \cdot (\mathbf {c} \times \mathbf {a} )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b} )}B) (a − b) 3 = a 3 − 3a 2 b 3ab 2 − b 3 c) ( x y ) 4 = x 4 4 x 3 y 6 x 2 y 2 4 xy 3 y 4 d) ( x − y ) 4 = x 4 − 4 x 3 y 6 x 2 y 2 − 4 xy 3 y 4



How To Develop A Numerical Differentiation Formula Using Taylor Expansion Series Mathematics Stack Exchange



Prove That The Following Determinant Is Equal To Ab Ca 3 B2 C2 Ac Ac C2 Brainly In



Misc 1 Find A B N In Expansion Of A B N If First Three


Academic Oup Com Ptp Article Pdf 13 4 405 13 4 405 Pdf


Http Ghcimdm4u Weebly Com Uploads 1 3 5 8 5 4 Pdf
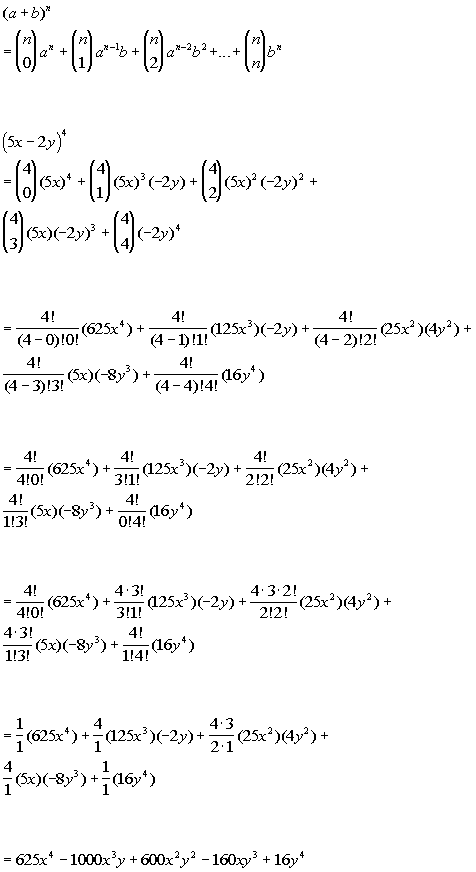


Wtamu Math Tutorials And Help



Illustration Of Imf Expansion Obtained Through Emd A C 1 T B C 2 Download Scientific Diagram



Solved Homework 3 Problem 1 Given F A B C D Acd A C Chegg Com


What Is The Expansion Of A B C 3 Quora



38 The Square Abcd Made Of 4 Metal Rods Ab Cd And Da Physics



What Are Various Forms To Write A B C A Whole Cube Quora



What Are Various Forms To Write A B C A Whole Cube Quora


Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau



Cs1022 Computer Programming Principles Ppt Video Online Download



Solved Question 1 Let A B And C Be 3 X 3 Matrices With D Chegg Com



1590 Bell Gossett Series B 2500 Expansion Tank Bladder Only



Lecture 34 Section 6 7 Wed Mar 28 Ppt Video Online Download



Solved Show That Det 1 1 1 1 A B C D A 2 B 2 C 2 D 2 A 3 Chegg Com
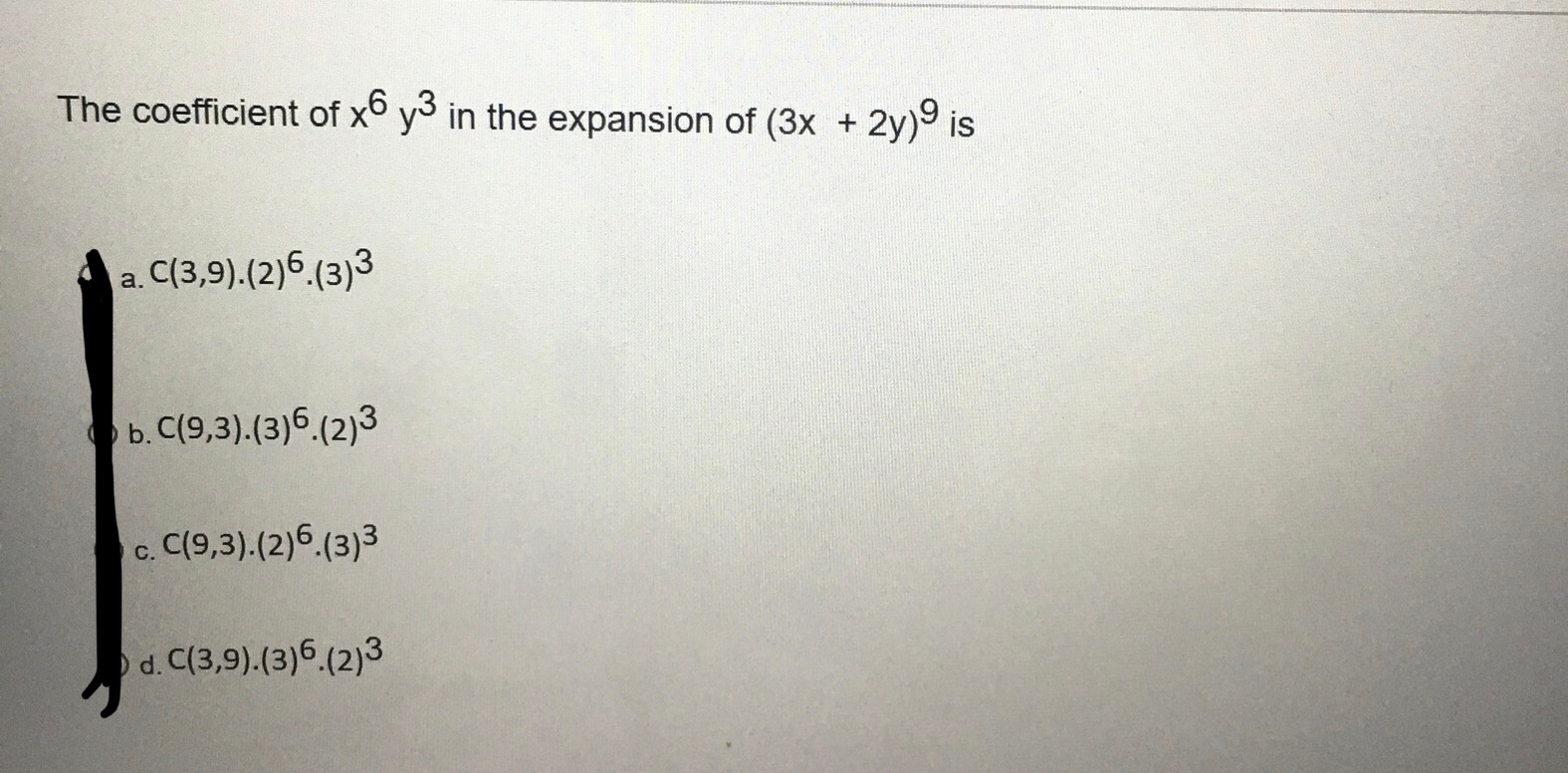


Solved The Coefficient Of Xo Y3 In The Expansion Of 3x Chegg Com



The Numerically Greatest Term In The Expansion Of 3 2x 9 When X 1 Is



The Coefficient Of A 7 B 10 C 3 In The Expansion Of Ab Ca 10 Is Brainly In



Binomial Expansion For Positive Integral Index Theorem Examples Video



Chemistry 231 Tutorial Session 2 Ca



Algebra Expansion And Factorisation
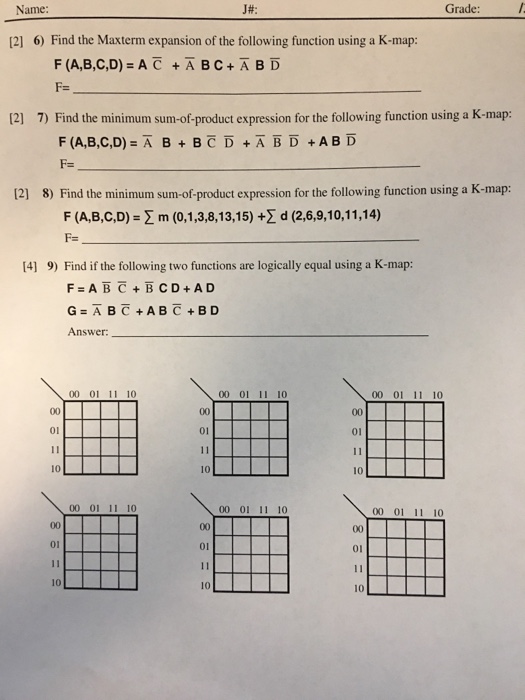


Solved Name J Grade 2 6 Find The Maxterm Expansion Of Chegg Com


What Is The Number Of Terms In A B C D 3 Quora



Solved 4 F A B C D A Ac D B Cd Ad Theorem Expand Chegg Com



Solved Engineering Analysis Of The Gas Expansion Factor Chegg Com



Solved 3 Find The Maxterm Expansion Of The Expression F Chegg Com


Math Cmu Edu Cnewstea Teaching Old Teaching 290fa18 Handouts 290fa18c18s Pdf



The Coefficient Of A 10b 7c 3 In The Expansion Of Ca Ab 10 Is


Plos Pathogens Eomes Cannot Replace Its Paralog T Bet During Expansion And Differentiation Of Cd8 Effector T Cells


What Is The Expansion Of A B C 3 Quora



Sporlan Thermostatic Expansion Valve Fbve 3 Cpj 3x4x2 Odf 30 For Sale Online Ebay


Solution Use The Binomial Theorem To Expand The Binomial And Express The Result In Simplified Form X 4 3


What Is The Formula Of A Cube Plus B Cube Plus C Cube Quora



Lesson 7 Expanding Products Of Algebraic Expressions Binomial Expansion Brilliant Maths



Ksfilsngaharam
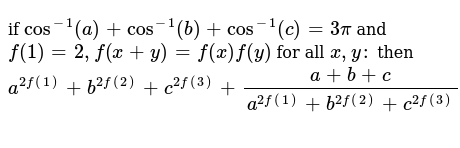


Which Expression Represents The Fourth Term In The Binomial Expan



The Trinomial Theorem And Pascal S Tetrahedron Exponents Now You Re Playing With Power


What Is The Expansion Of A B C 3 Quora



Special Product And Expansion If A B C 11 And Ab Ca 36 Find The Value Of A 2 B 2 C 2


Www Selfstudys Com Uploads Pdf Fpp7u4bssw85pz9qsk4y Pdf



Expansion Of A B C 3 Brainly In


What Is The Expansion Of A B C 3 Quora


Q Tbn And9gcsectilf2waloldhrvvptyk0gppw0kxl9fe R8 Qft5iyl5p4g2 Usqp Cau



What Is The Expansion Of A B C 3 Quora



Solved Verify The Expansion Of The Vector Triple Product Chegg Com
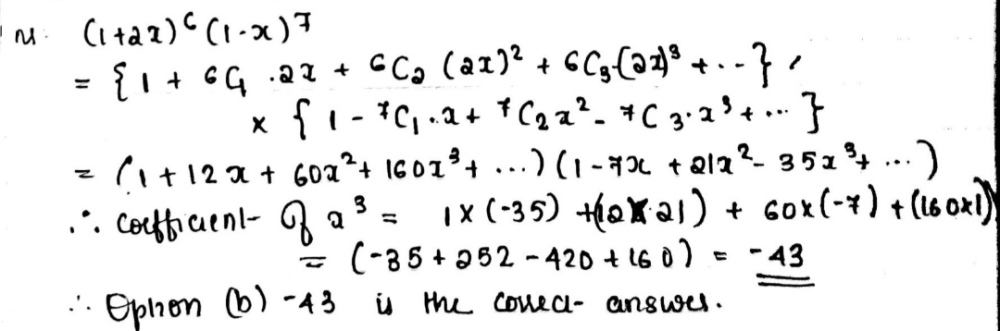


Question The Coefficient If X 3 In The Expansion Of 1 2x 6 1 X 7 Is A 43 B 43 C 63 D 63 Snapsolve



What Are Various Forms To Write A B C A Whole Cube Quora


A Volume Expansion And B Density Of Il As A Function Of Mole Download Scientific Diagram



The Trinomial Theorem And Pascal S Tetrahedron Exponents Now You Re Playing With Power



Amazon Com The Cambridge Ancient History Volume 3 Part 3 The Expansion Of The Greek World Eighth To Sixth Centuries Boardman John Hammond N G L Books


A 3 B 3 C 3



Solved Project 1 Part A You Are Tasked To Calculate A Spe Chegg Com


Http Www Ee Uidaho Edu Ee Power Brian Digital Ece240 Sampleexams Exam1sol Pdf


2


S3 Eu West 1 Amazonaws Com S3 Euw1 Ap Pe Ws4 Cws Documents Ri Prod Mcqs Quiz 18 Pdf



Linear Algebra Week 7 Port Exercises Reals Express The Following Fractions Studocu


Search Q A 5e3 2bb 5e3 2bc 5e3 Formula Tbm Isch


Web Pa Msu Edu People Pratts Phy231 Exams Extraproblems Ch10 Pdf



B C D E G I J 39 Write The Taylor Expansion Of Function F Order N At To Given Below 1 Homeworklib



Lancaster Joe S Math Class Blog Expansion And Factorisation



Thermal Expansion Behavior Of A B Ti 50pt C D Ti 37 5pt 12 5ir Download Scientific Diagram



Find The Coefficient Of A 2 B 3 C 4 D In The Expansion Of A B C D 10 Youtube


What Is The Expansion Of A B C 3 Quora



Solved Question Sc12 1 C3 Using The Binomial Theorem E Chegg Com



The Expansions Of Algebraic Expression By Opening Bracket


What Is The Formula For Math A B C 3 Math Quora



What Is A B 3 Quora



コメント
コメントを投稿